Disclaimer
I should start by saying that I’m not a crypto expert, just an engineer who needs to understand enough how something works in order to be able to use it effectively. So, this is written with the intention that it’s explanatory rather than reference material. The benefit of this is that this article is maths-free (I won’t mention the Discrete Logarithm Problem): keep reading!
Why use ECC?
I want to be able to do security properly, but for IoT applications RSA keys are rather large and hard to handle. To save power, I would rather transmit as few bytes as possible over a radio link, and larger data can cause buffer size problems, or not fit into a single network packet. ECC has much smaller key sizes, and should improve this.
How much smaller are ECC keys?
This is a subject that can cause endless discussion, but we need to start somewhere: To give an idea of the difference, a 256-bit ECC key can be considered equivalent to a 3072-bit RSA key. ECC keys are much smaller than RSA keys.
Why do I care how it works?
It can be tedious to get crypto to work at all; any mistake and it is very hard to debug—this is one of many good arguments for using existing libraries. However it can be hard to get the output from one library/platform/language to work with another. For an IoT application, you’re unlikely to be using the same library on your embedded device as on your cloud server.
This isn’t trivial even with secret key encryption; for example one library uses an AES key as you supplied it, another hashes it first. And then there are many padding schemes, etc. We can expect ECC to be harder.
I need to be able to understand the steps that the data goes through, to have a chance of being able to debug any integration problems.
RSA we know
I feel that I’ve got a working understanding of RSA en/decryption; generating a secret key based on a pair of large pseudoprimes, and a public key from their product. Then doing encryption by modular exponentiation using the public key, or a signature using the private key. The message isn’t directly encrypted using RSA, instead a temporary secret/symmetric key is generated and used to encrypt the message; this key can be efficiently encrypted using RSA and transmitted with the message. Decryption or verification simply use the opposite key than the original operation.
In my mind, I think of RSA having primitives; keygen, encrypt, decrypt, sign, verify. (Or maybe just; keygen, do_modular_exponentiation.)
ECC is more different than I expected
Looking at the interface to my ECC hardware, or software library, I find it supports a different set of primitives than I expected; keygen of course, and I can see ECDSA Sign and ECDSA Verify, but the only other operation is ECDH (Elliptic Curve Diffie Helman). There is no encrypt or decrypt operation!
ECIES
ECC encrypt is not a primitive operation. Instead we can use ECDH (Elliptic Curve Diffie Helman) to generate a shared secret, and use this as a secret key. This is called ECIES (Elliptic Curve Integrated Encryption Scheme).
ECIES “how it works”
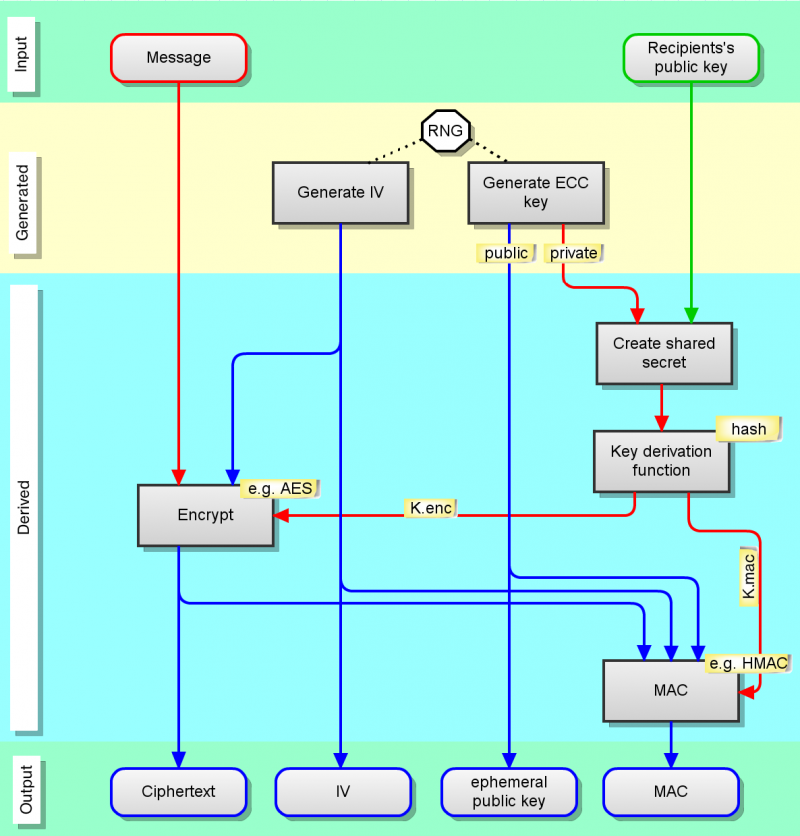
The descriptions you’ll find of ECIES may well be correct, but I didn’t find them immediately useful. I drew a diagram to understand it, and here’s a tidied-up copy of it.
ECIES Steps:
- inputs are the plaintext message, and the recipient’s ECC public key
- an IV (initialisation vector) is generated (random bytes)
- an ephemeral ECC key is generated (random bytes). The public key is derived from the private key
- the ephemeral private key is combined with the recipient’s public key – this is the ECDH shared secret
- the shared secret is stretched using a KDF (key derivation function) to create 2 secret keys
- one secret key is used to encrypt the plaintext
- the other secret key is used to generate a MAC
- the output is ciphertext + the IV + the ephemeral public key + the MAC
Notes/comments:
- with RSA, generating a keypair is slow – you need to search for & test big pseudoprimes. However with ECC it’s quick & simple, just random bytes (with minor constraints). This is why it’s possible to generate an ephemeral key for each encryption.
- the Key Derivation Function isn’t as complicated as password-based KDFs are; for example, ANSI-X9.63-KDF with a hash generating the same number of bits as you need for encryption is just:
hash(secret || 0x01) || hash(secret || 0x02) - the recipient can decrypt the ciphertext because he can recreate the shared secret, using his private key, and the ephemeral public key. So he can recreate Kenc and Kmac to check the MAC & decrypt. With this, and an understanding of the encryption flow, it’s clear how decryption can work, so not worth including as a separate diagram.
- for any ECC system you need to pick a specific curve. Be aware that there are multiple names in common use for some curves, and confusingly similar names for some different curves.
- as well as agreeing a curve (including size), the sender & recipient also need to agree on many other properties, including:
- input padding
- Key Derivation Function
- hash function (+ size)
- encryption function (+ size)
- MAC function (+ size)
- encoding of transmitted data
- unfortunately the details are not well standardised. For example, Crypto++ and Bouncy Castle don’t interoperate by default because they use a different wordsize for a length when calculating the MAC.
Conclusion
Having drawn & redrawn the diagram for this post, ECC encryption now seems a lot clearer to me than when I started. If you’re wondering why I bothered to write this, then that’s a success.
References
“A Survey of the Elliptic Curve Integrated Encryption Scheme” – Journal of Compute Science and Engineering, Vol 2 Iss 1 Aug 2010